Maxima graph: различия между версиями
Tora-bora (обсуждение | вклад) |
Ivzeivze (обсуждение | вклад) Нет описания правки |
||
| (не показано 10 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
{{review | {{review | ||
|Title = Статья-шпаргалка по построению 2D графиков в системе компьютерной математики wxMaxima | |Title = Статья-шпаргалка по построению 2D графиков в системе компьютерной математики wxMaxima | ||
|Annotation = В этой заметке кратко описано построение простых | |Annotation = В этой заметке кратко описано построение простых двумерных графиков при помощи системы компьютерной алгебры Maxima | ||
|Author = And | |Author = And | ||
|Tag = | |Tag = | ||
|Section = практика | |Section = практика | ||
|Issue = | |Issue =01 | ||
}} | }} | ||
{{review-nav | {{review-nav | ||
|link= | |link=http://www.altlinux.org/Books:Maxima Компьютерная математика с Maxima | ||
|link2=http://mydebianblog.blogspot.ru/search/label/%D0%B3%D0%BD%D1%83%D0%BF%D0%BB%D0%BE%D1%82 Записки дебианщика | |||
}} | }} | ||
Основу системы образуют три стандартные программы: | |||
* '''maxima''' — математическое ядро с интерфейсом командной строки; | |||
* '''wxMaxima''' — графический интерфейс пользователя; | |||
* '''gnuplot''' — мощная утилита для построения научных графиков. | |||
Рассмотрим как с ними работать. | |||
== Запуск ядра из командной строки == | |||
Программа '''maxima''', запущенная из терминала, не поддерживает редактирование набранных команд и прокрутку истории, как, например, интерпретатор '''bash''' или '''python'''. Для удобства использования следует вызывать её в readline-обёртке: '''rlwrap maxima'''. | |||
Обёртка '''rlwrap''' запускает '''maxima''' как дочерний процесс, фильтрует ввод-вывод и перенаправляет сигналы, реализуя недостающую функциональность. | |||
== Команды построения графиков == | == Команды построения графиков == | ||
| Строка 18: | Строка 27: | ||
<source lang = matlab>plot2d ([f1, f2], [x, xmin, xmax], [y, ymin, ymax], [опция 1], [опция 2], [и т.д.])</source> | <source lang = matlab>plot2d ([f1, f2], [x, xmin, xmax], [y, ymin, ymax], [опция 1], [опция 2], [и т.д.])</source> | ||
График выводится новом окне средствами утилиты gnuplot. Чтобы построить нескольких графиков внутри документа wxMaxima служит другая команда '''wxplot2d''' с теми же опциями. | График выводится в новом окне средствами утилиты gnuplot. Чтобы построить нескольких графиков внутри документа wxMaxima, служит другая команда '''wxplot2d''' с теми же опциями. | ||
Функции f могут быть: | Функции f могут быть: | ||
*явными выражениями вида f(x); | *явными выражениями вида <tt>f(x)</tt>; | ||
*зависящими от параметра вида [parametric, x(t), y(t), [t, tmin, tmax]]; | *зависящими от параметра вида <tt>[parametric, x(t), y(t), [t, tmin, tmax]]</tt>; | ||
*дискретным набором точек [discrete, point_list] | *дискретным набором точек <tt>[discrete, point_list]</tt>. | ||
== Виды функций и примеры их графиков == | == Виды функций и примеры их графиков == | ||
| Строка 29: | Строка 38: | ||
=== Явная функция в прямоугольных координатах === | === Явная функция в прямоугольных координатах === | ||
Нарисуем графики функций десятичного логарифма, косинуса, тангенса | Нарисуем графики функций десятичного логарифма, косинуса, тангенса и кубического корня на отрезке от 0 до 2,5π: | ||
<source lang = matlab> | |||
(%i1) | (%i1) | ||
/* Определим десятичный логарифм через натуральный */ | /* Определим десятичный логарифм через натуральный */ | ||
| Строка 42: | Строка 51: | ||
По умолчанию цвета графиков из списка функций следующие: | По умолчанию цвета графиков из списка функций следующие: | ||
1 | 1 — синий (blue), 2 — красный (red), 3 — зеленый (green), 4 — пурпурный (magenta), 5 — черный(black), 6 — голубой (cyan). | ||
При большем числе графиков их цвета циклически повторяются. | При большем числе графиков их цвета циклически повторяются. | ||
| Строка 48: | Строка 57: | ||
=== Явная функция в полярных координатах === | === Явная функция в полярных координатах === | ||
Для построения надо определить связь между полярными радиусом r и углом φ | Для построения надо определить связь между полярными радиусом r и углом φ, а также использовать опцию gnuplot '''set polar''': | ||
<source lang = matlab> | <source lang = matlab> | ||
(%i1) | (%i1) | ||
| Строка 62: | Строка 71: | ||
'''Кусочно-линейная функция''' может быть задана при помощи оператора '''if then else''' вида: | '''Кусочно-линейная функция''' может быть задана при помощи оператора '''if then else''' вида: | ||
'''if''' условие1 '''then''' выражение1 '''else''' выражение2 | '''if''' условие1 '''then''' выражение1 '''else''' выражение2. | ||
Например построим графики функций [[Файл:Maxima_graph_func.png]] и g(x)=sin(5x)-1 | Например, построим графики функций [[Файл:Maxima_graph_func.png]] и g(x)=sin(5x)-1: | ||
<source lang = matlab> | <source lang = matlab> | ||
(%i1) | (%i1) | ||
| Строка 76: | Строка 85: | ||
Результат показан на Рис.2А. | Результат показан на Рис.2А. | ||
'''Функция заданная параметрически''' строится при помощи опции '''parametric'''. | '''Функция, заданная параметрически''', строится при помощи опции '''parametric'''. | ||
Построим фигуру Лиссажу внутри окружности. | Построим фигуру Лиссажу внутри окружности. | ||
Уравнение окружности x=5*cos(t), y=5*sin(t) | * Уравнение окружности x=5*cos(t), y=5*sin(t); | ||
Уравнение фигуры x=3*cos(4t), y=3*sin(3t) | * Уравнение фигуры x=3*cos(4t), y=3*sin(3t). | ||
<source lang = matlab> | <source lang = matlab> | ||
(%i1) | (%i1) | ||
| Строка 89: | Строка 98: | ||
],[x,-8,8], [y,-8,8], [gnuplot_preamble,"set size ratio 1"]) $ | ],[x,-8,8], [y,-8,8], [gnuplot_preamble,"set size ratio 1"]) $ | ||
</source> | </source> | ||
Результат показан на Рис.2Б. Здесь использованы две необязательные опции. Первая | Результат показан на Рис.2Б. Здесь использованы две необязательные опции. Первая — '''nticks''', которая задает число точек графика, и вторая опция программы gnuplot — '''set size ratio 1''', устанавливающая одинаковые масштабы по осям графика (в противном случае вместо окружности рисуется эллипс). | ||
[[Файл:Maxima_graph03.png|thumb|left|400px|Рис. 2А]][[Файл:Maxima_graph04.png|thumb|center|400px|Рис. 2Б]] | [[Файл:Maxima_graph03.png|thumb|left|400px|Рис. 2А]][[Файл:Maxima_graph04.png|thumb|center|400px|Рис. 2Б]] | ||
| Строка 96: | Строка 105: | ||
=== Дискретные функции === | === Дискретные функции === | ||
Для вывода дискретных данных служит опция '''discrete'''. Данные можно задавать либо в виде 2-х отдельных списков аргументов [xi] и значений [yi] | Для вывода дискретных данных служит опция '''discrete'''. Данные можно задавать либо в виде 2-х отдельных списков аргументов [xi] и значений [yi] либо в виде вложенного списка с координатами точек [xi,yi]: | ||
<source lang = matlab> | <source lang = matlab> | ||
(%i1) xlist:[1,2,3,4,5,6,7] $ | (%i1) xlist:[1,2,3,4,5,6,7] $ | ||
| Строка 106: | Строка 115: | ||
</source> | </source> | ||
[[Файл:Maxima_graph05.png|center|300px]] | [[Файл:Maxima_graph05.png|center|300px]] | ||
Опция '''style''' | Опция '''style''' задаёт вид графиков: в виде линий, точек или линий с точками. | ||
Опция '''gnuplot_term''' с выбранными параметрами сохраняет изображение в графическеский файл формата png размером 300 на 200 пикселов, '''gnuplot_out_file''' задает имя файла. | Опция '''gnuplot_term''' с выбранными параметрами сохраняет изображение в графическеский файл формата png размером 300 на 200 пикселов, '''gnuplot_out_file''' задает имя файла. | ||
| Строка 113: | Строка 122: | ||
Для записи списка данных в файл служит функция '''write_data'''(список, ''адрес'', разделитель). | Для записи списка данных в файл служит функция '''write_data'''(список, ''адрес'', разделитель). | ||
Разделителем может быть запятая | Разделителем может быть запятая — '''comma''', вертикальная черта — '''pipe''' , точка с запятой — '''semicolon''' и пробел — '''space''' (он принят по умолчанию). Например, команда write_data(xy,"./data.txt") запишет в текущий каталог текстовый файл с именем data.txt, содержащий список координат точек, которые будут разделены пробелами. | ||
Чтобы получить данные служит функция '''read_nested_list'''(''адрес'', разделитель) | Чтобы получить данные, служит функция '''read_nested_list'''(''адрес'', разделитель). | ||
Она читает файл как список вложенных списков, образованных элементами очередной строки. | Она читает файл как список вложенных списков, образованных элементами очередной строки. | ||
Простой список создается командой '''read_list'''. | Простой список создается командой '''read_list'''. | ||
| Строка 141: | Строка 150: | ||
=== Надписи и заголовки === | === Надписи и заголовки === | ||
Название графика задается командой gnuplot внутри опции '''gnupot_preamble'''. Команды gnuplot пишутся внутри общих кавычек | Название графика задается командой gnuplot внутри опции '''gnupot_preamble'''. Команды gnuplot пишутся внутри общих кавычек и отделяются друг от друга точкой с запятой: | ||
<tt>[gnuplot_preamble, '''"set title 'имя графика' ; "''']</tt> | <tt>[gnuplot_preamble, '''"set title 'имя графика' ; "''']</tt>; | ||
Названия осей <tt>'''[xlabel, "имя для оси x"], [ylabel, "имя для оси у"]'''</tt> | Названия осей <tt>'''[xlabel, "имя для оси x"], [ylabel, "имя для оси у"]'''</tt>; | ||
Подписи кривых (легенда ) <tt>'''[legend, "кривая 1", "кривая 2", "и т. д."]'''</tt> | Подписи кривых (легенда ) <tt>'''[legend, "кривая 1", "кривая 2", "и т. д."]'''</tt>. | ||
Легенда выводятся в правом верхнем углу, изменить | Легенда выводятся в правом верхнем углу, изменить её положение можно командой gnuplot '''set key''': | ||
<tt>'''set key bottom'''</tt> — внизу | <tt>'''set key bottom'''</tt> — внизу; | ||
<tt>'''set key top left'''</tt> — вверху слева | <tt>'''set key top left'''</tt> — вверху слева; | ||
<tt>'''set key bottom center outside'''</tt> — внизу по центру за пределами графика | <tt>'''set key bottom center outside'''</tt> — внизу по центру за пределами графика. | ||
Пара замечаний о | Пара замечаний о выводе русских надписей при работе wxMaxima в ALT Linux. | ||
Кириллические буквы в легенде значительно увеличивают ее размеры, а команда wxplot2d | Кириллические буквы в легенде значительно увеличивают ее размеры, а команда wxplot2d не может отобразить русские литеры, так как не находит шрифт Arial. Для устранения последней проблемы надо установить в систему шрифты Microsoft, скомандовав в консоли (от имени root): | ||
<code>apt-get install fonts-ttf-ms</code>. | |||
'''Шкалы и линии сетки''' можно менять при помощи следующих команд gnuplot [1]: | '''Шкалы и линии сетки''' можно менять при помощи следующих команд gnuplot [1]: | ||
<tt>'''set grid'''</tt> — отображает сетку | <tt>'''set grid'''</tt> — отображает сетку; | ||
<tt>'''set grid polar df'''</tt> — задает радиальную сетку в полярной системе координат, df угол между ее линиями в радианах | <tt>'''set grid polar df'''</tt> — задает радиальную сетку в полярной системе координат, df угол между ее линиями в радианах; | ||
<tt>'''set xtics dx; set ytics dy'''</tt> — указание шага между основными линиями сетки (по x шаг=dx, по y шаг=dy | <tt>'''set xtics dx; set ytics dy'''</tt> — указание шага между основными линиями сетки (по x шаг=dx, по y шаг=dy); | ||
<tt>'''set border 3; set xtics nomirror'''</tt> — убирает отражение оси х сверху | <tt>'''set border 3; set xtics nomirror'''</tt> — убирает отражение оси х сверху; | ||
<tt>'''set mxtics n'''</tt> — разбивает основные деления шкалы по оси х на n интервалов | <tt>'''set mxtics n'''</tt> — разбивает основные деления шкалы по оси х на n интервалов; | ||
<tt>'''set size ratio m'''</tt> — рисует размер оси y в m раз больше размера оси х | <tt>'''set size ratio m'''</tt> — рисует размер оси y в m раз больше размера оси х; | ||
<tt>'''set log x; set log y'''</tt> — отображает шкалы на оси координат в логарифмическом масштабе | <tt>'''set log x; set log y'''</tt> — отображает шкалы на оси координат в логарифмическом масштабе. | ||
'''Пример.''' Построим графики некоторых специальных функций | '''Пример.''' Построим графики некоторых специальных функций: интегрального косинуса Ci(x), интегрального синуса Si(x), функции ошибок erf(x) и дополнительной функции ошибок erfc(x): | ||
<source lang = matlab> | <source lang = matlab> | ||
(%i1) | (%i1) | ||
| Строка 263: | Строка 272: | ||
|} | |} | ||
Стиль кривой можно задавать словесно через последовательность опций color, style, point_type | Стиль кривой можно задавать словесно через последовательность опций color, style, point_type либо кратко при помощи кодовых параметров. | ||
Пример: '''[color, red, black]''', '''[style , lines, points]''', '''[point_type, plus]'''. | |||
Линии имеют 2 параметра — толщина, цвет. | Линии имеют 2 параметра — толщина, цвет. | ||
| Строка 275: | Строка 282: | ||
У линий с точками 4 параметра — толщина линии, размер точки, цвет, тип точки. | У линий с точками 4 параметра — толщина линии, размер точки, цвет, тип точки. | ||
Тот же пример: '''[style, [lines,1,2], [points, 3, 5, 3]]''' | Тот же пример: '''[style, [lines,1,2], [points, 3, 5, 3]]'''. | ||
=== Сглаживание графиков === | === Сглаживание графиков === | ||
| Строка 281: | Строка 288: | ||
При построении графиков в виде линий с точками метки часто расположены слишком густо и кривые получаются «мохнатыми». Это можно исправить подобрав параметры '''nticks''' (задает начальное число точек) и '''adapt_depth''' (число проходов алгоритма сглаживания). | При построении графиков в виде линий с точками метки часто расположены слишком густо и кривые получаются «мохнатыми». Это можно исправить подобрав параметры '''nticks''' (задает начальное число точек) и '''adapt_depth''' (число проходов алгоритма сглаживания). | ||
Для примера нарисуем график испускательной способности (мощности излучаемой единицей поверхности в единичном частотном интервале) абсолютно черного тела | Для примера нарисуем график испускательной способности (мощности излучаемой единицей поверхности в единичном частотном интервале) абсолютно черного тела r (T,ν). | ||
Согласно формуле Планка: | Согласно формуле Планка: | ||
| Строка 287: | Строка 294: | ||
[[Файл:Plank.png]] | [[Файл:Plank.png]] | ||
где T | где T — температура, ν — частота, с — скорость света, h — постоянная Планка, k — постоянная Больцмана. | ||
<source lang = matlab> | <source lang = matlab> | ||
(%i1) /* Физические константы и формула*/ | (%i1) /* Физические константы и формула*/ | ||
| Строка 311: | Строка 318: | ||
__SHOWFACTBOX__ | __SHOWFACTBOX__ | ||
[[Категория:ALT-review | [[Категория:ALT-review]] | ||
{{Category navigation|title=Журнал ALT-review|category=ALT-review|sortkey={{SUBPAGENAME}}}} | |||
Текущая версия от 08:30, 15 февраля 2016
Журнал ALT-review
Title::Статья-шпаргалка по построению 2D графиков в системе компьютерной математики wxMaxima- Автор: Author::And Раздел: Section::практика Выпуск: Issue::01

| ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

| ||||||||||||||||||||||
| ||||||||||||||||||||||
Основу системы образуют три стандартные программы:
- maxima — математическое ядро с интерфейсом командной строки;
- wxMaxima — графический интерфейс пользователя;
- gnuplot — мощная утилита для построения научных графиков.
Рассмотрим как с ними работать.
Запуск ядра из командной строки
Программа maxima, запущенная из терминала, не поддерживает редактирование набранных команд и прокрутку истории, как, например, интерпретатор bash или python. Для удобства использования следует вызывать её в readline-обёртке: rlwrap maxima. Обёртка rlwrap запускает maxima как дочерний процесс, фильтрует ввод-вывод и перенаправляет сигналы, реализуя недостающую функциональность.
Команды построения графиков
Построение графиков осуществляет команда plot2d с аргументами в виде списка функций, координат и необязательных опций построения:
plot2d ([f1, f2], [x, xmin, xmax], [y, ymin, ymax], [опция 1], [опция 2], [и т.д.])
График выводится в новом окне средствами утилиты gnuplot. Чтобы построить нескольких графиков внутри документа wxMaxima, служит другая команда wxplot2d с теми же опциями.
Функции f могут быть:
- явными выражениями вида f(x);
- зависящими от параметра вида [parametric, x(t), y(t), [t, tmin, tmax]];
- дискретным набором точек [discrete, point_list].
Виды функций и примеры их графиков
Явная функция в прямоугольных координатах
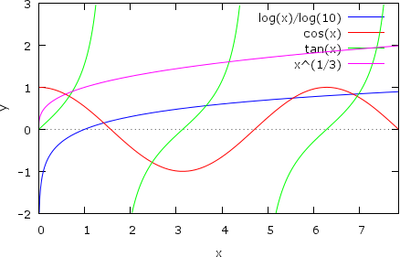
Нарисуем графики функций десятичного логарифма, косинуса, тангенса и кубического корня на отрезке от 0 до 2,5π:
(%i1)
/* Определим десятичный логарифм через натуральный */
log10(x):=log(x)/log(10) $
(%i2)
/* Строим графики */
plot2d([log10(x), cos(x), tan(x), x^(1/3)], [x, 0, 2.5*%pi], [y, -2, 3]) $
Результат показан на Рис 1А. По умолчанию цвета графиков из списка функций следующие:
1 — синий (blue), 2 — красный (red), 3 — зеленый (green), 4 — пурпурный (magenta), 5 — черный(black), 6 — голубой (cyan).
При большем числе графиков их цвета циклически повторяются.
Явная функция в полярных координатах
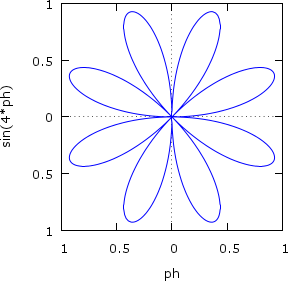
Для построения надо определить связь между полярными радиусом r и углом φ, а также использовать опцию gnuplot set polar:
(%i1)
r(ph):=sin(4*ph);
(%i2)
plot2d([r(ph)],[ph,0,2*%pi],[x,-1,1],[y,-1,1],[gnuplot_preamble,"set polar"]);
Результат показан на Рис. 1Б.
Кусочно-линейная функция может быть задана при помощи оператора if then else вида:
if условие1 then выражение1 else выражение2.
Например, построим графики функций  и g(x)=sin(5x)-1:
и g(x)=sin(5x)-1:
(%i1)
f(x):= if x<-2 then 8
else if x<0 then -x^3
else x^3 $
g: sin(5*x)-1 $
plot2d([g,f],[x,-5,2],[y,-3,10]);
Результат показан на Рис.2А.
Функция, заданная параметрически, строится при помощи опции parametric.
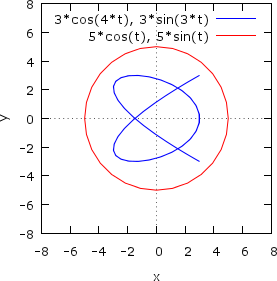
Построим фигуру Лиссажу внутри окружности.
- Уравнение окружности x=5*cos(t), y=5*sin(t);
- Уравнение фигуры x=3*cos(4t), y=3*sin(3t).
(%i1)
plot2d([ [parametric,3*cos(4*t),3*sin(3*t),[t,-10,10],[nticks,300]],
[parametric,5*cos(t),5*sin(t),[t,-%pi,%pi] ]
],[x,-8,8], [y,-8,8], [gnuplot_preamble,"set size ratio 1"]) $
Результат показан на Рис.2Б. Здесь использованы две необязательные опции. Первая — nticks, которая задает число точек графика, и вторая опция программы gnuplot — set size ratio 1, устанавливающая одинаковые масштабы по осям графика (в противном случае вместо окружности рисуется эллипс).
Дискретные функции
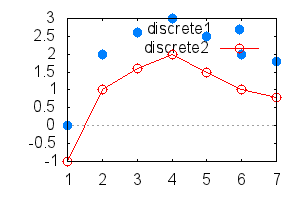
Для вывода дискретных данных служит опция discrete. Данные можно задавать либо в виде 2-х отдельных списков аргументов [xi] и значений [yi] либо в виде вложенного списка с координатами точек [xi,yi]:
(%i1) xlist:[1,2,3,4,5,6,7] $
ylist:[0,2,2.6,3,2.5,2,1.8] $
xy:[[1,-1],[2,1],[3,1.6],[4,2],[5,1.5],[6,1],[7,0.8]] $
(%i2) plot2d([ [discrete,xlist,ylist],[discrete,xy] ],[style,points,linespoints],
[gnuplot_term, "png size 300,200" ],[gnuplot_out_file,"data.png"]);
Опция style задаёт вид графиков: в виде линий, точек или линий с точками.
Опция gnuplot_term с выбранными параметрами сохраняет изображение в графическеский файл формата png размером 300 на 200 пикселов, gnuplot_out_file задает имя файла.
Чтение и запись данных в файл
Для записи списка данных в файл служит функция write_data(список, адрес, разделитель). Разделителем может быть запятая — comma, вертикальная черта — pipe , точка с запятой — semicolon и пробел — space (он принят по умолчанию). Например, команда write_data(xy,"./data.txt") запишет в текущий каталог текстовый файл с именем data.txt, содержащий список координат точек, которые будут разделены пробелами.
Чтобы получить данные, служит функция read_nested_list(адрес, разделитель). Она читает файл как список вложенных списков, образованных элементами очередной строки. Простой список создается командой read_list.
(%i3) data:read_nested_list("./data.txt");
[[1,-1],[2,1],[3,1.6],[4,2],[5,1.5],[6,1],[7,0.8]]
(%i4) single:read_list("./data.txt");
[1,-1,2,1,3,1.6,4,2,5,1.5,6,1,7,0.8]
Заметим, что если указать формат файла csv (стандартный формат принятый для числовых данных), то разделителем по умолчанию станет запятая, а не пробел.
Запись графика в файл
Для этого надо указать тип графического терминала [gnuplot_term, тип ] и имя выходного фала [gnuplot_out_file, " имя"]. Тип может быть либо ps (формат post script) либо один из графических форматов png, jpg и т.п. Если не указывать имя выходного файла, то будет применено стандартное имя maxplot.
[gnuplot_term, ps], [gnuplot_out_file, "data.eps"] — выводит изображение в формате post script в файл data.eps
[gnuplot_term, jpg] — сохраняет изображение стандартного размера в файл с именем maxplot.jpg
[gnuplot_term, "gif size 400,400" ], [gnuplot_out_file,"data.gif"]) — создает gif файл размером 400 на 400 пискселей.
Опции оформления
Надписи и заголовки
Название графика задается командой gnuplot внутри опции gnupot_preamble. Команды gnuplot пишутся внутри общих кавычек и отделяются друг от друга точкой с запятой:
[gnuplot_preamble, "set title 'имя графика' ; "];
Названия осей [xlabel, "имя для оси x"], [ylabel, "имя для оси у"];
Подписи кривых (легенда ) [legend, "кривая 1", "кривая 2", "и т. д."].
Легенда выводятся в правом верхнем углу, изменить её положение можно командой gnuplot set key:
set key bottom — внизу;
set key top left — вверху слева;
set key bottom center outside — внизу по центру за пределами графика.
Пара замечаний о выводе русских надписей при работе wxMaxima в ALT Linux.
Кириллические буквы в легенде значительно увеличивают ее размеры, а команда wxplot2d не может отобразить русские литеры, так как не находит шрифт Arial. Для устранения последней проблемы надо установить в систему шрифты Microsoft, скомандовав в консоли (от имени root):
apt-get install fonts-ttf-ms.
Шкалы и линии сетки можно менять при помощи следующих команд gnuplot [1]:
set grid — отображает сетку;
set grid polar df — задает радиальную сетку в полярной системе координат, df угол между ее линиями в радианах;
set xtics dx; set ytics dy — указание шага между основными линиями сетки (по x шаг=dx, по y шаг=dy);
set border 3; set xtics nomirror — убирает отражение оси х сверху;
set mxtics n — разбивает основные деления шкалы по оси х на n интервалов;
set size ratio m — рисует размер оси y в m раз больше размера оси х;
set log x; set log y — отображает шкалы на оси координат в логарифмическом масштабе.
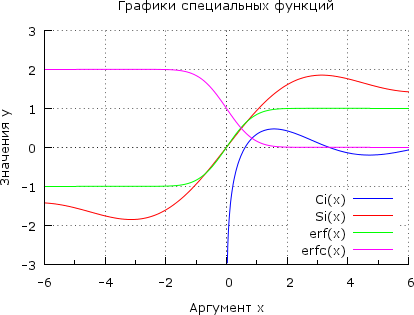
Пример. Построим графики некоторых специальных функций: интегрального косинуса Ci(x), интегрального синуса Si(x), функции ошибок erf(x) и дополнительной функции ошибок erfc(x):
(%i1)
plot2d([expintegral_ci(x),expintegral_si(x),erf(x),erfc(x)], [x,-6,6], [y,-3,3],[gnuplot_preamble, "set grid;set title 'Графики специальных функций';
set key bottom; set border 3; set xtics nomirror; set ytics nomirror; set mxtics 2;"],
[xlabel,"Аргумент x"],[ylabel,"Значения y"],[legend,"Ci(x)","Si(x)","erf(x)","erfc(x)"])$
Стили графиков
Кривые можно строить в виде линий lines, линий с точками linespoints и точек points. Цвета могут задаваться словесно или кодом согласно таблице:
| Cиний | Красный | Зеленый | Пурпурный | Черный | Голубой |
| blue | red | green | magenta | black | cyan |
| 1 | 2 | 3 | 4 | 5 | 6 |
Тип точек также может задаваться словесно или кодом:
| ● | ○ | + | X | * | ■ | □ | ▲ | ∆ | ▼ | ∇ | ♦ | ◊ |
| bullet | circle | plus | times | asterisk | box | square | triangle | delta | wedge | nabla | diamond | lozenge |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
Стиль кривой можно задавать словесно через последовательность опций color, style, point_type либо кратко при помощи кодовых параметров.
Пример: [color, red, black], [style , lines, points], [point_type, plus].
Линии имеют 2 параметра — толщина, цвет.
У точки 3 параметра — размер, цвет, тип точки.
У линий с точками 4 параметра — толщина линии, размер точки, цвет, тип точки.
Тот же пример: [style, [lines,1,2], [points, 3, 5, 3]].
Сглаживание графиков
При построении графиков в виде линий с точками метки часто расположены слишком густо и кривые получаются «мохнатыми». Это можно исправить подобрав параметры nticks (задает начальное число точек) и adapt_depth (число проходов алгоритма сглаживания).
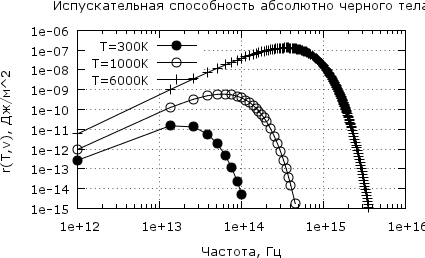
Для примера нарисуем график испускательной способности (мощности излучаемой единицей поверхности в единичном частотном интервале) абсолютно черного тела r (T,ν).
Согласно формуле Планка:
где T — температура, ν — частота, с — скорость света, h — постоянная Планка, k — постоянная Больцмана.
(%i1) /* Физические константы и формула*/
k:1.38e-23 $ h:6.6e-34 $ c:3e8 $
r(T,v):=2*%pi*h*v^3/(c^2*(exp(h*v/(k*T))-1));
(%2)plot2d([ r(3e2,v),r(1e3,v),r(6e3,v) ],[v,1e12,1e16],[y,1e-15,1e-6],
[xlabel,"Частота, Гц"],[ylabel, "r(T,v), Дж/м^2 " ],
[legend,"T=300K"," T=1000K"," T=6000K"],
[color,black],[style, linespoints],[point_type,bullet,circle,plus],[nticks,50],[adapt_depth,2],
[gnuplot_preamble, "set log x; set log y; set mxtics 10; set grid; set key left; set title 'Испускательная способность абсолютно черного тела';" ]);
По возможности следует избегать расчетов и построений с очень большими или малыми величинами. В противном случае могут возникнуть проблемы с переполнением разрядов. Если в данном примере задать логарифмический масштаб не через опции gnuplot, а напрямую, как [logx], [logy], то Maxima откажется строить график вследствие ошибки переполнения.
Литература
- Е.А. Чичкарев. Компьютерная математика с Maxima. Руководство для школьников и студентов. http://www.altlinux.org/Books:Maxima
- Записки Дебианщика. http://mydebianblog.blogspot.ru/search/label/гнуплот
__SHOWFACTBOX__